[10000ダウンロード済み√] ���角形 の 相似 条件 証明 325129

三角形の相似条件と基本的な証明 無料で使える中学学習プリント

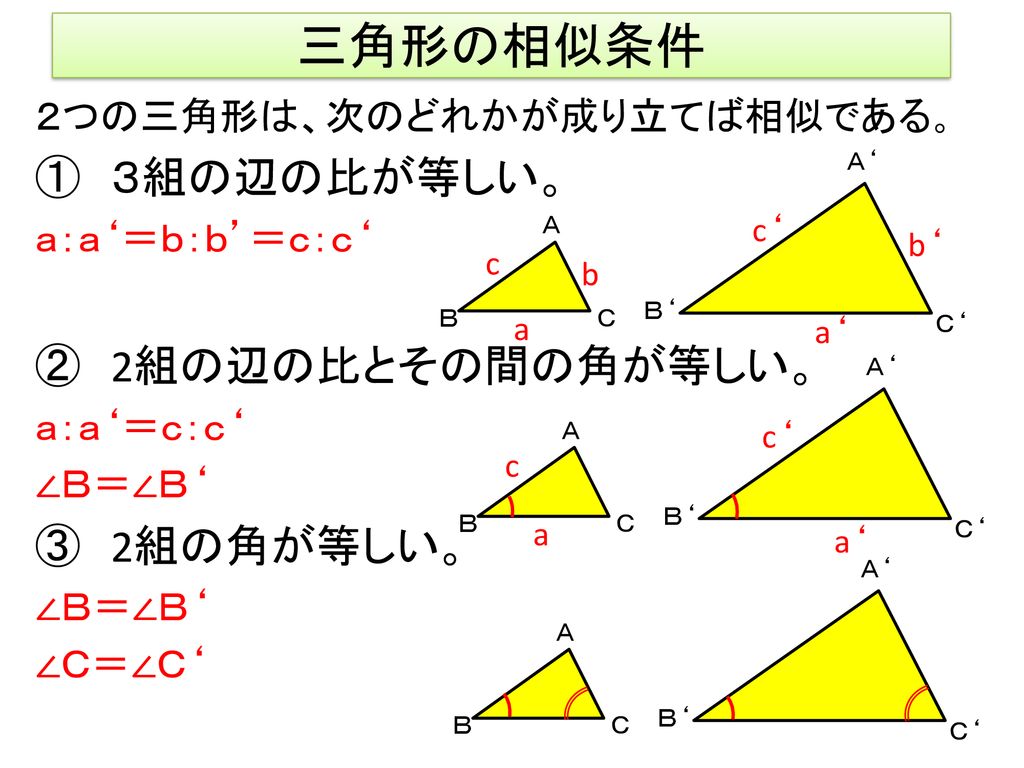
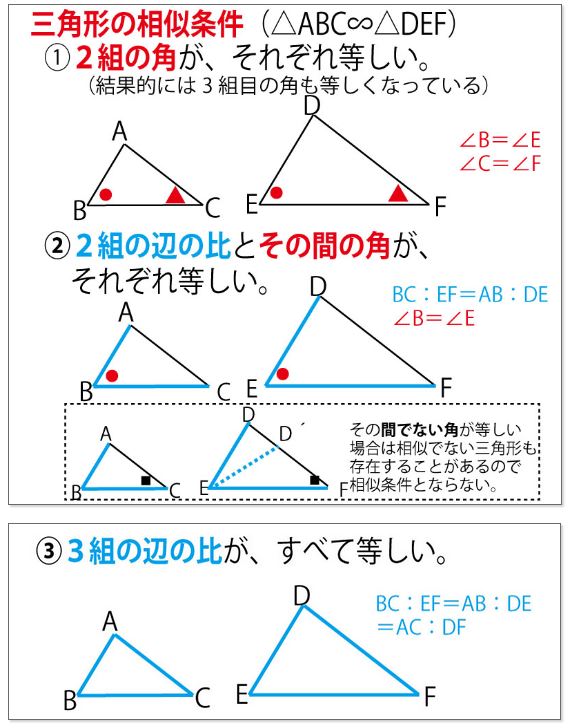
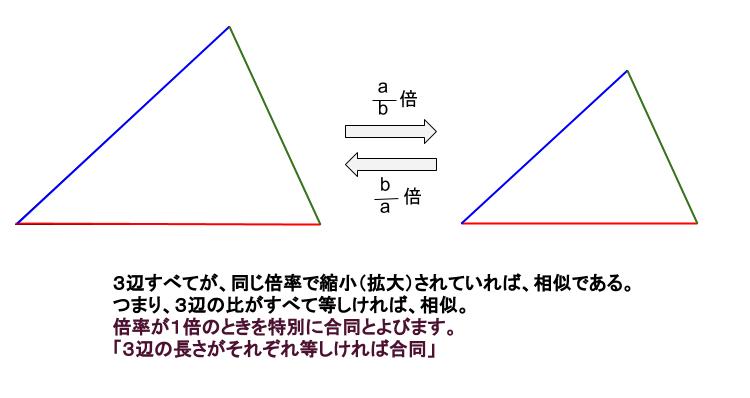
 三角形の相似条件 ① 3 組の辺の比がそれぞれ等しい;「図形の中から相似な三角形を見出し、相似条件を用いて証明することができる。 2つの三角形は、次のどれかが成り立てば相似である。 ① 3組の辺の比が等しい。

三角形 の 相似 条件 証明

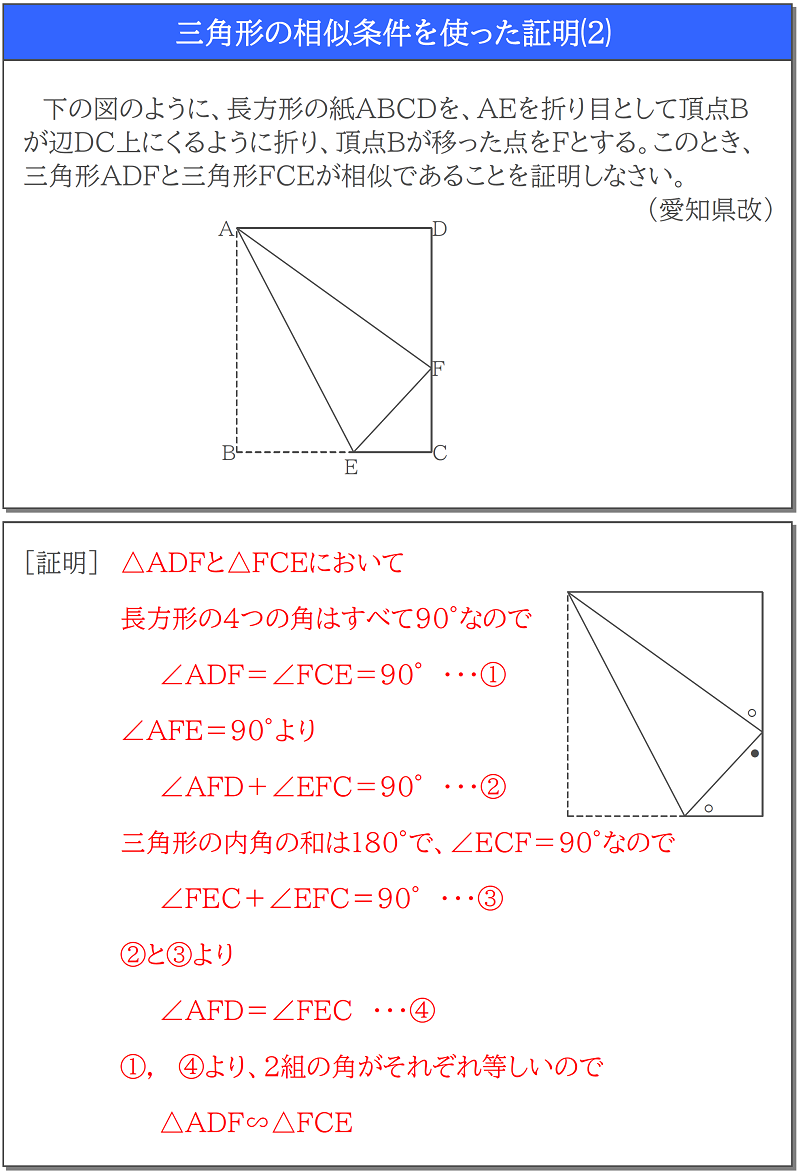
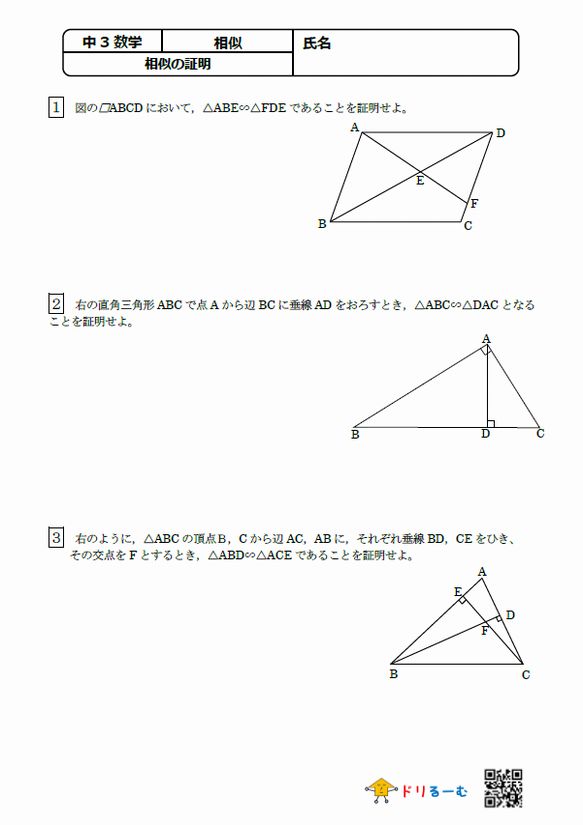
三角形 の 相似 条件 証明- 相似の証明で使うこと 相似の証明をするにあたって、∠DAF = x°とおきます。このように、自分で、どの角の大きさを文字で表すのかを宣言しておくことが大切になります。 三角形の相似条件 2組の角がそれぞれ等しい 二等辺三角形の定義動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru

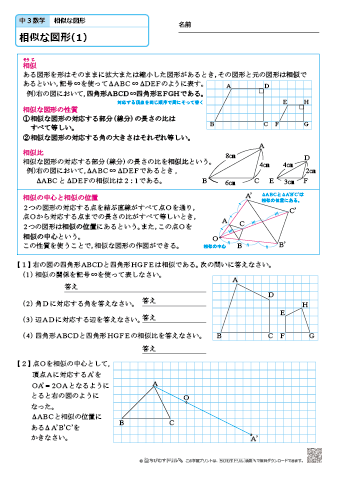
中学３年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

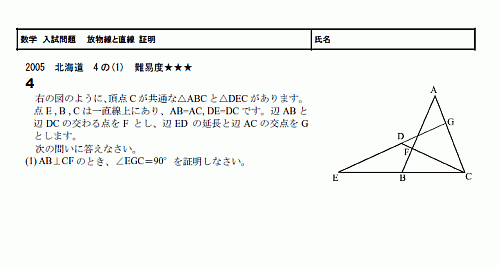
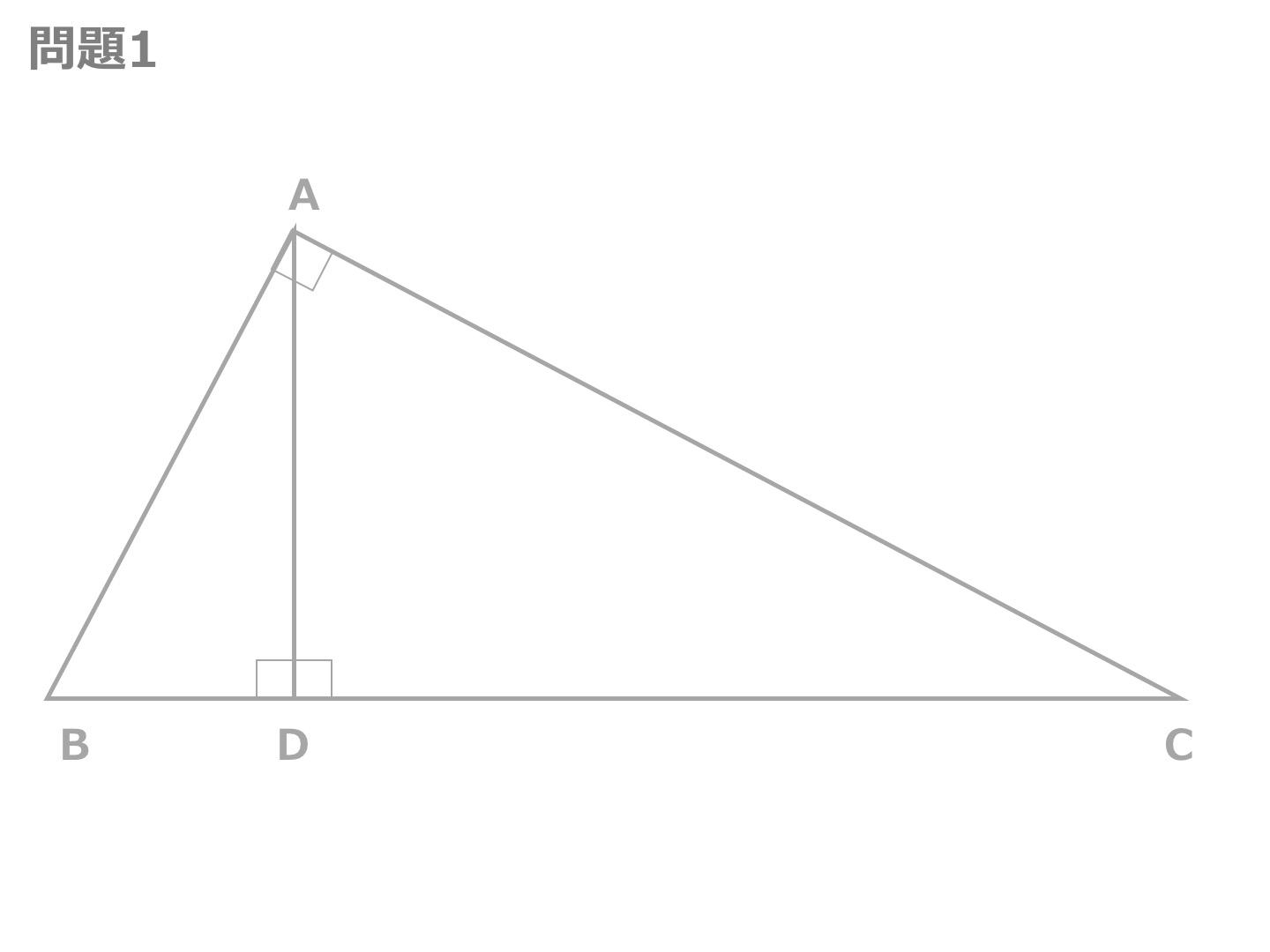
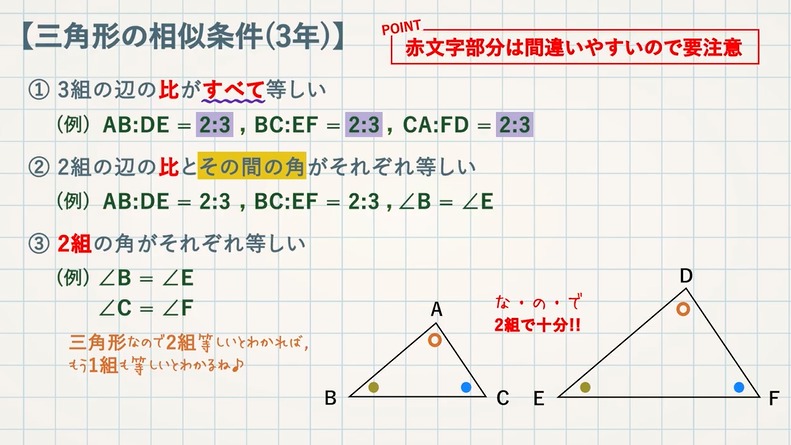
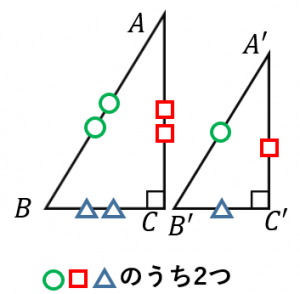
三角形の相似条件 三角形の相似条件 とは、2つの三角形が相似であることを示すための条件です。 以下の3つの相似条件のうち、どれかが成り立つ場合、その三角形は相似であるといえます。 3組の辺の比がすべて等しい。 2組の辺の比が等しく、その間の角が等しい。 2組の角がそれぞれ等しい。 このページの続きでは、三角形の図を見ながら、これらの相似条件相似の証明・直角三角形型 直角三角形が関わる有名図形配置について学習します。 例題1 下の図のように、直角三角形 \(abc\) において、点 \(a\) から辺 \(bc\) に向かって垂線をひき、辺 \(bc\) との交点を \(d\) とします。4 直角三角形の相似が成り立つ2つの条件 41 直角三角形の相似が成り立つ条件①：斜辺と1つの鋭角がそれぞれ等しい

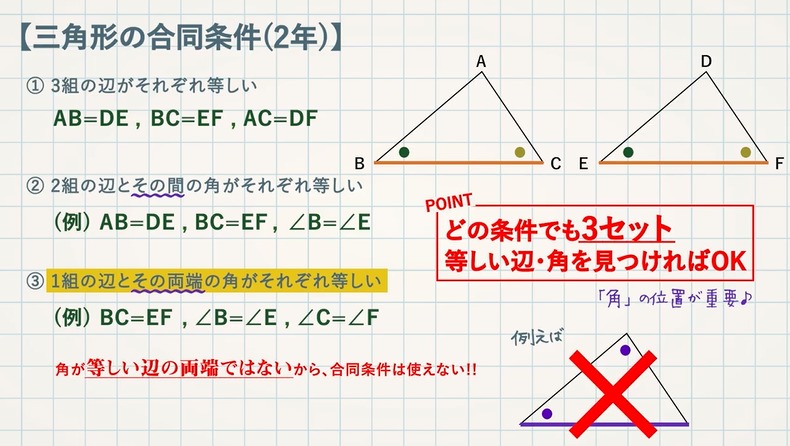
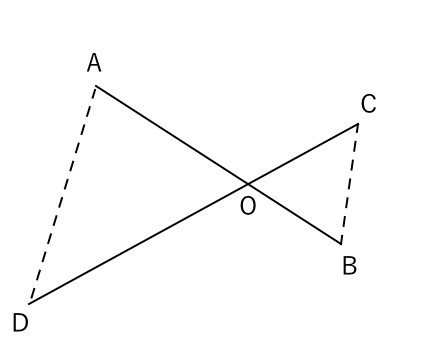
 三角形の相似条件 証明問題で最も出題されるのがこの相似の証明です。 使う相似条件は99％「2組の角がそれぞれ等しい」と言って過言ではありません。 とにかく等しい角を2つ見つけることを心がけてください。 中3 学習単元一覧 式の展開 因数分解 平方根 2次方程式 2乗に比例する関数 図形の相似 三平方の定理 円の性質 標本調査 私立高校入試対策 公立高校入試対策 式の展開式の展開の基 では、どのような時に合同と言えるのか？ それは次の3角形の合同条件の3つのどれかが満たされる時です。 （あとで登場する相似条件と混同しないように！ ） 三角形の合同条件 3辺の長さがそれぞれ等しい 2辺の長さとその間の角がそれぞれ等しい 1辺

三角形 の 相似 条件 証明のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似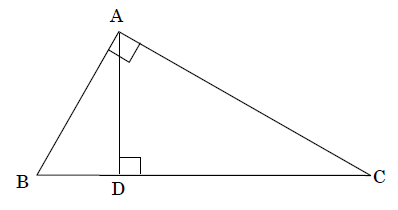
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	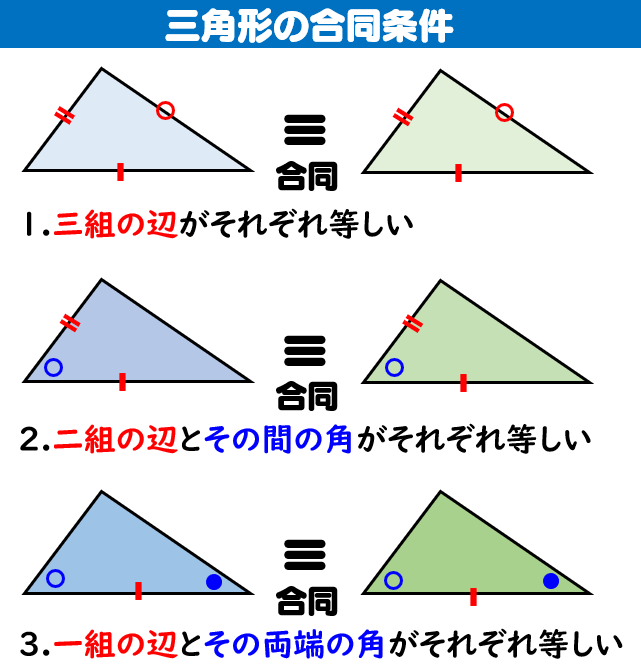世界一わかりやすい数学問題集中３ ５章 図形と相似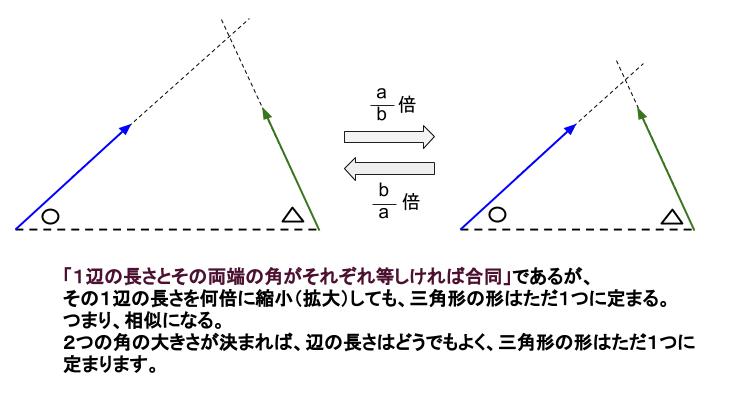
世界一わかりやすい数学問題集中３ ５章 図形と相似	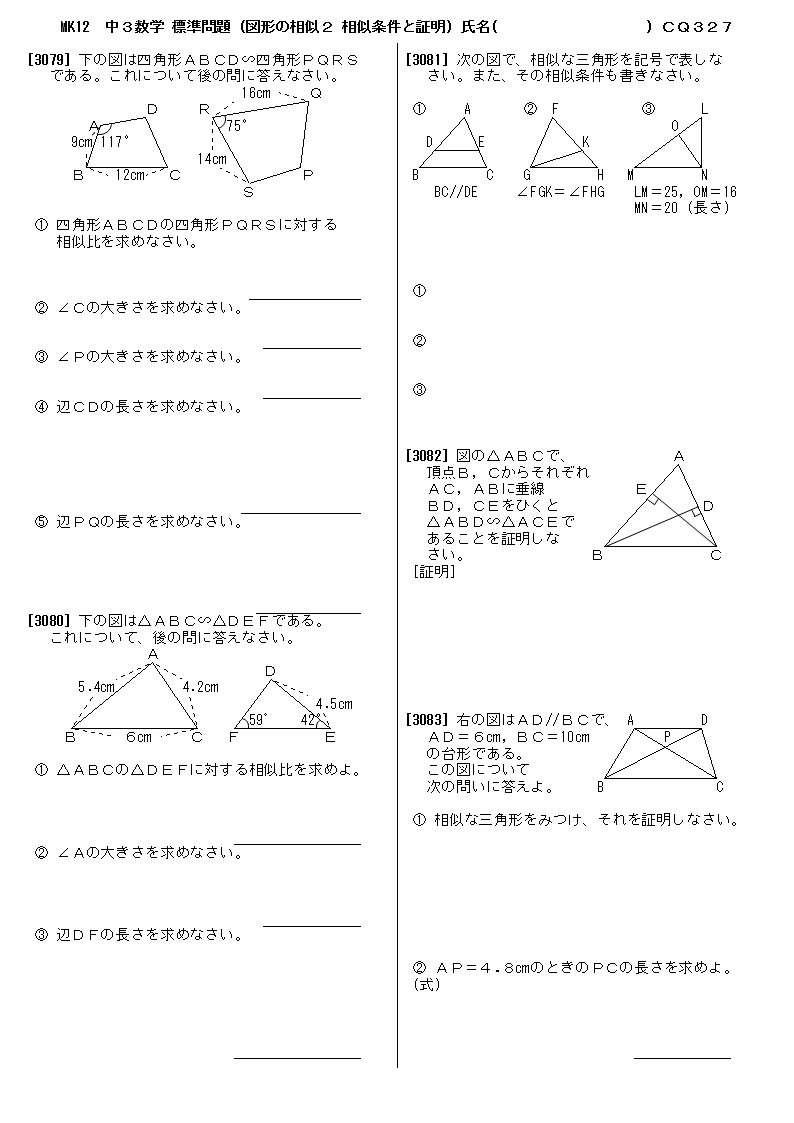世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	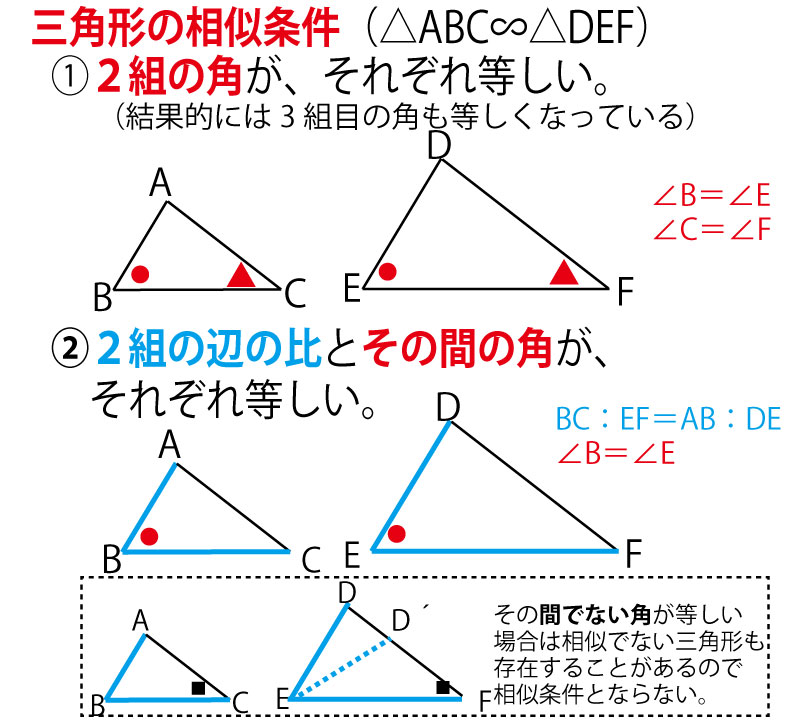世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	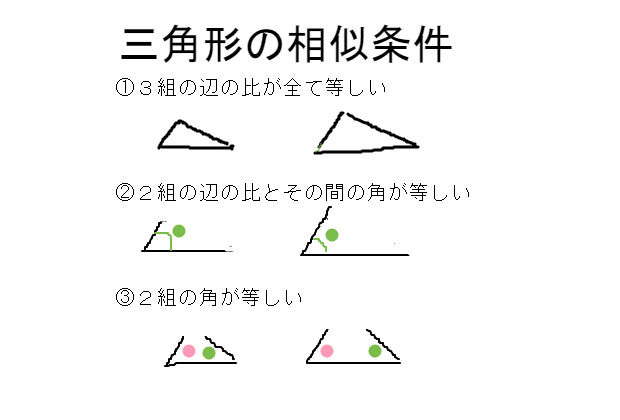世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	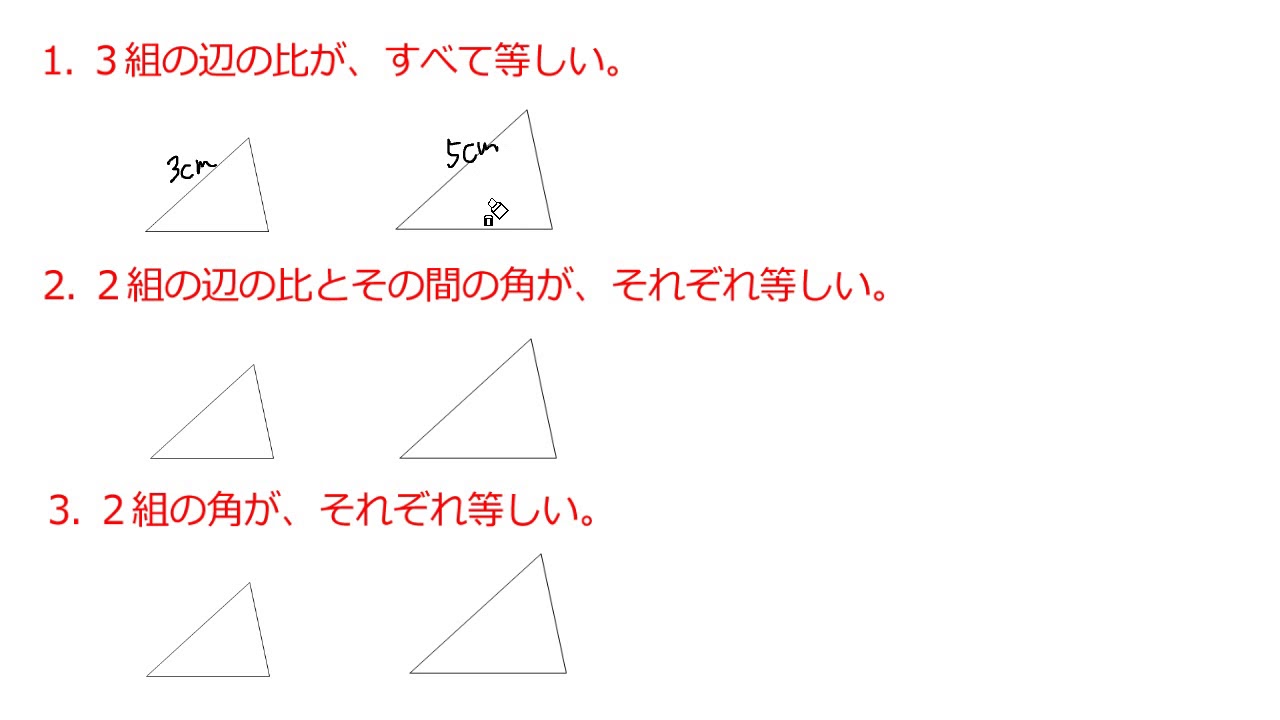世界一わかりやすい数学問題集中３ ５章 図形と相似	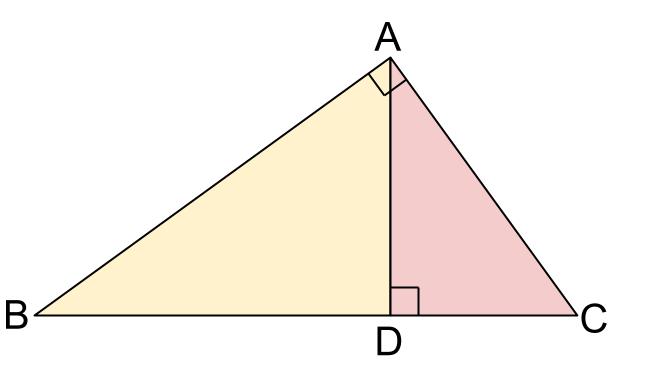世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	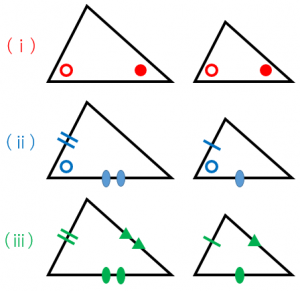世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	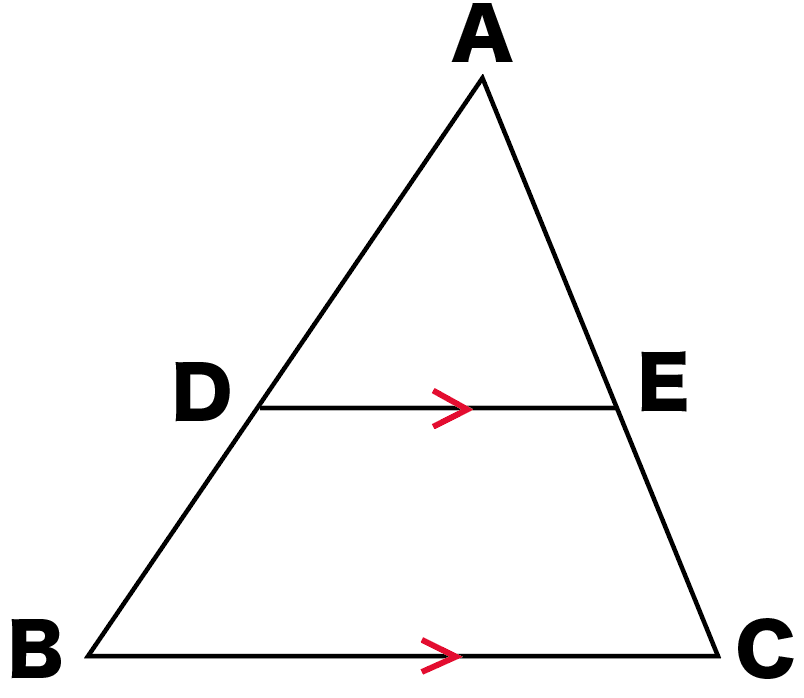世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	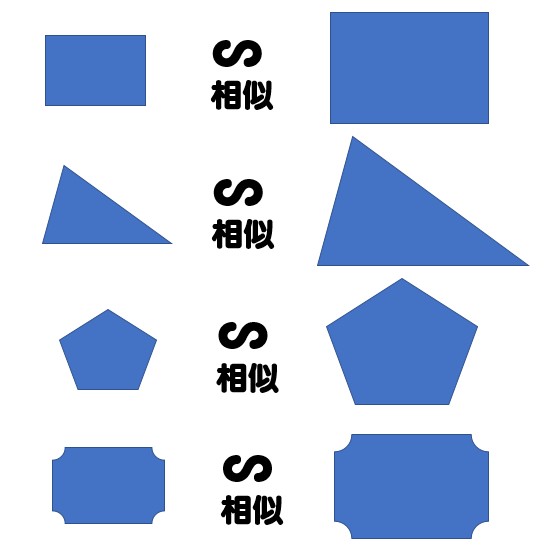世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	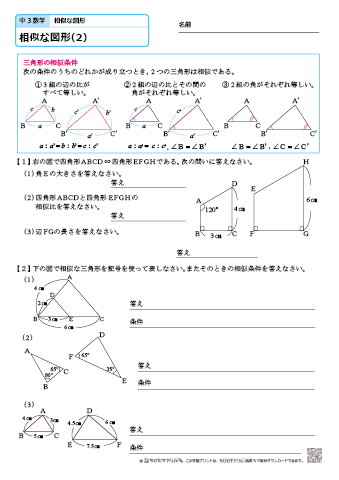世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	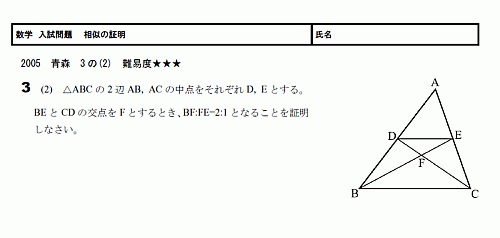世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	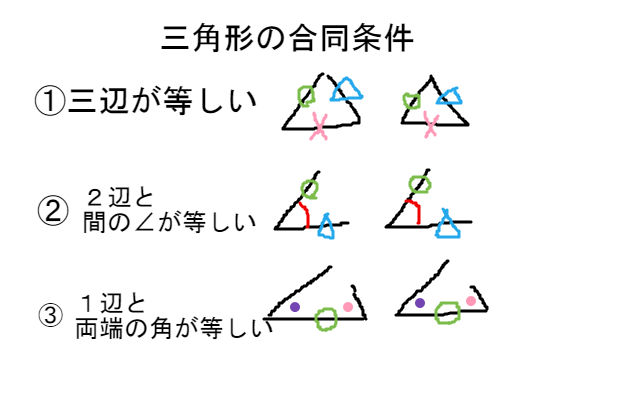世界一わかりやすい数学問題集中３ ５章 図形と相似	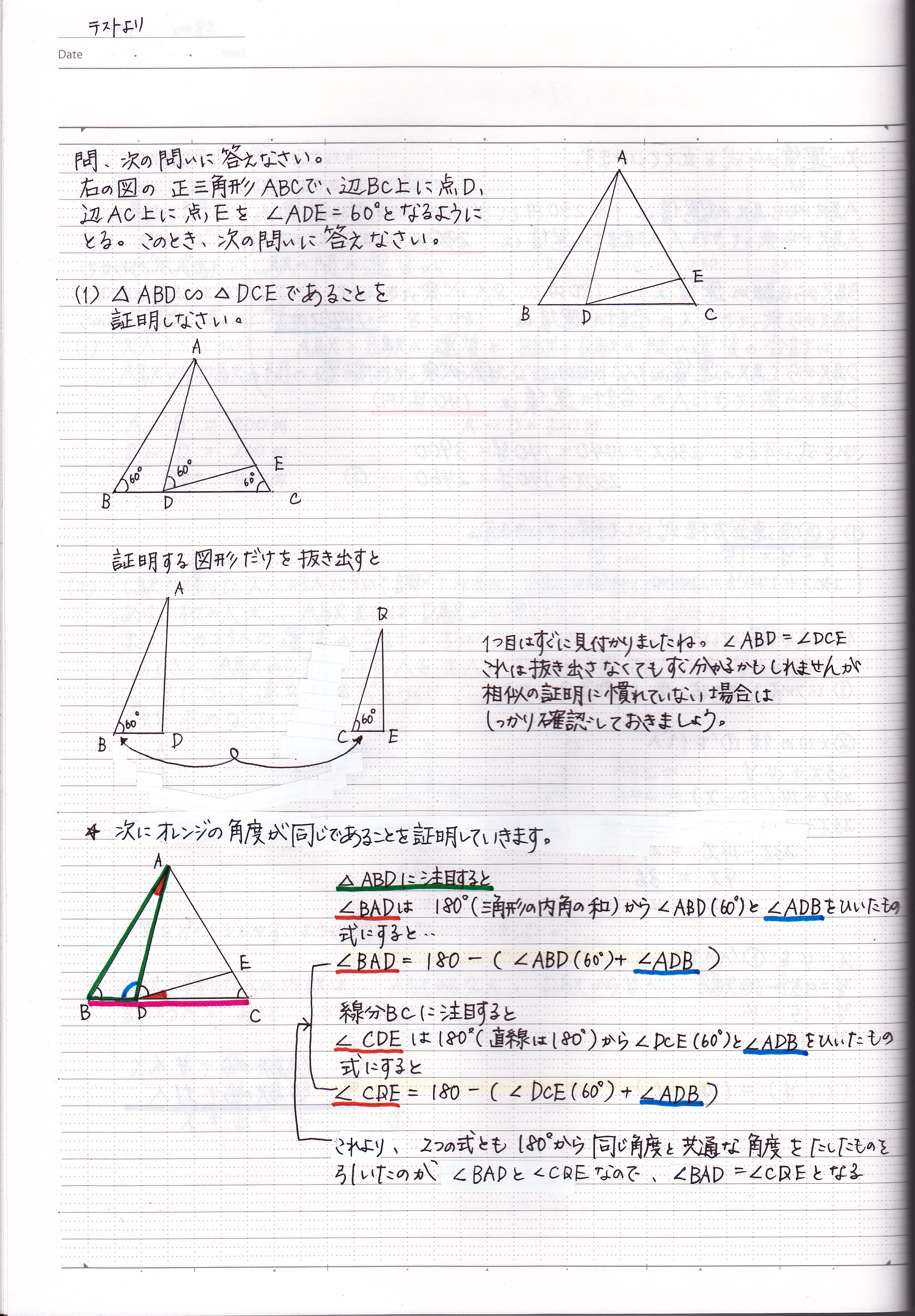世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	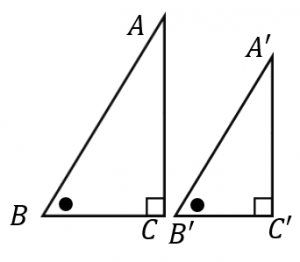世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	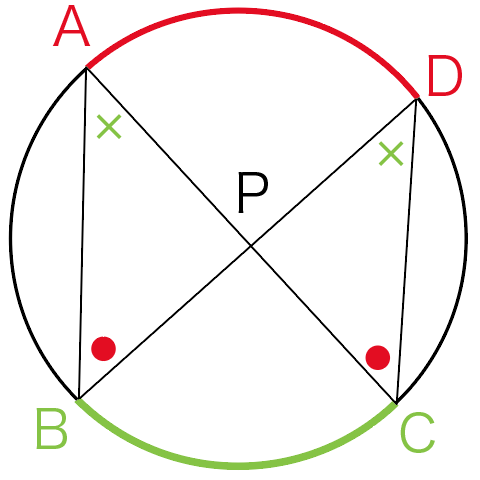世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	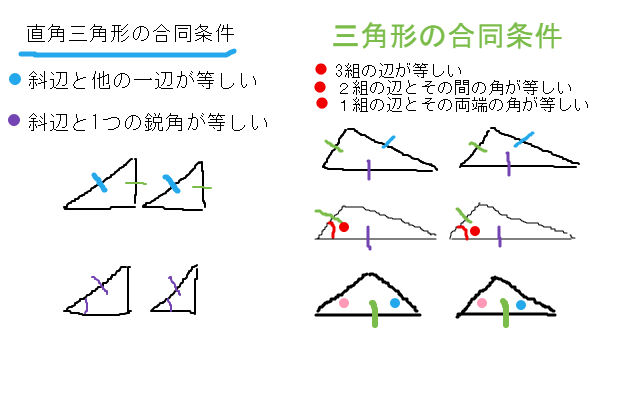世界一わかりやすい数学問題集中３ ５章 図形と相似	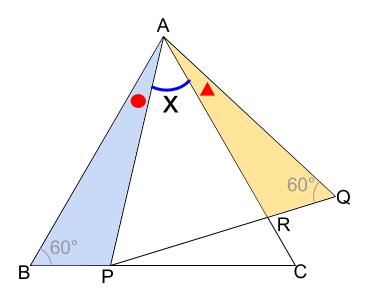世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	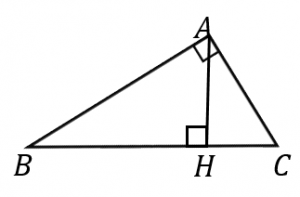世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	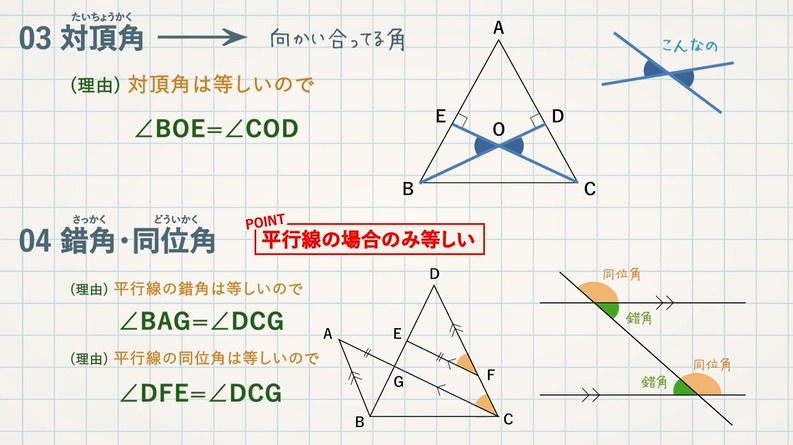世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	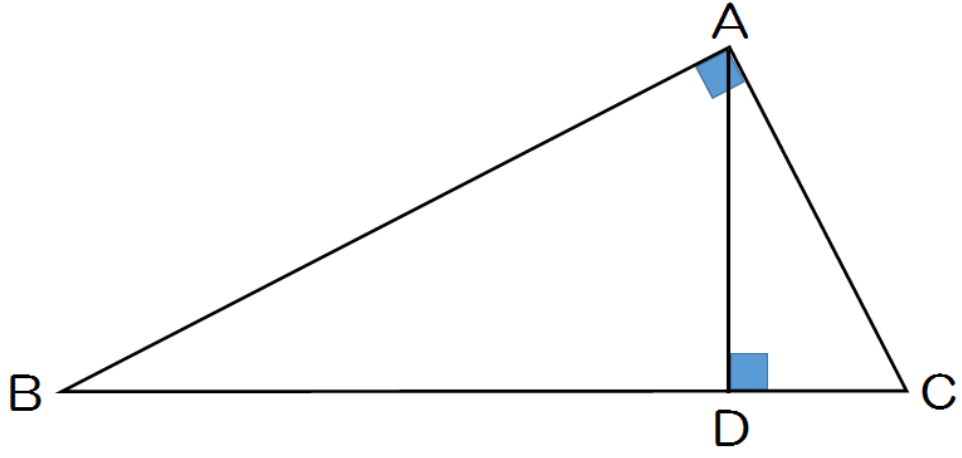世界一わかりやすい数学問題集中３ ５章 図形と相似	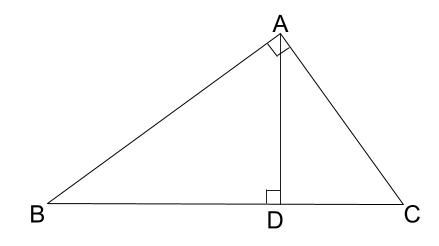世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	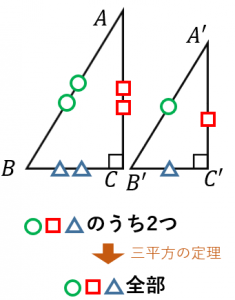世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	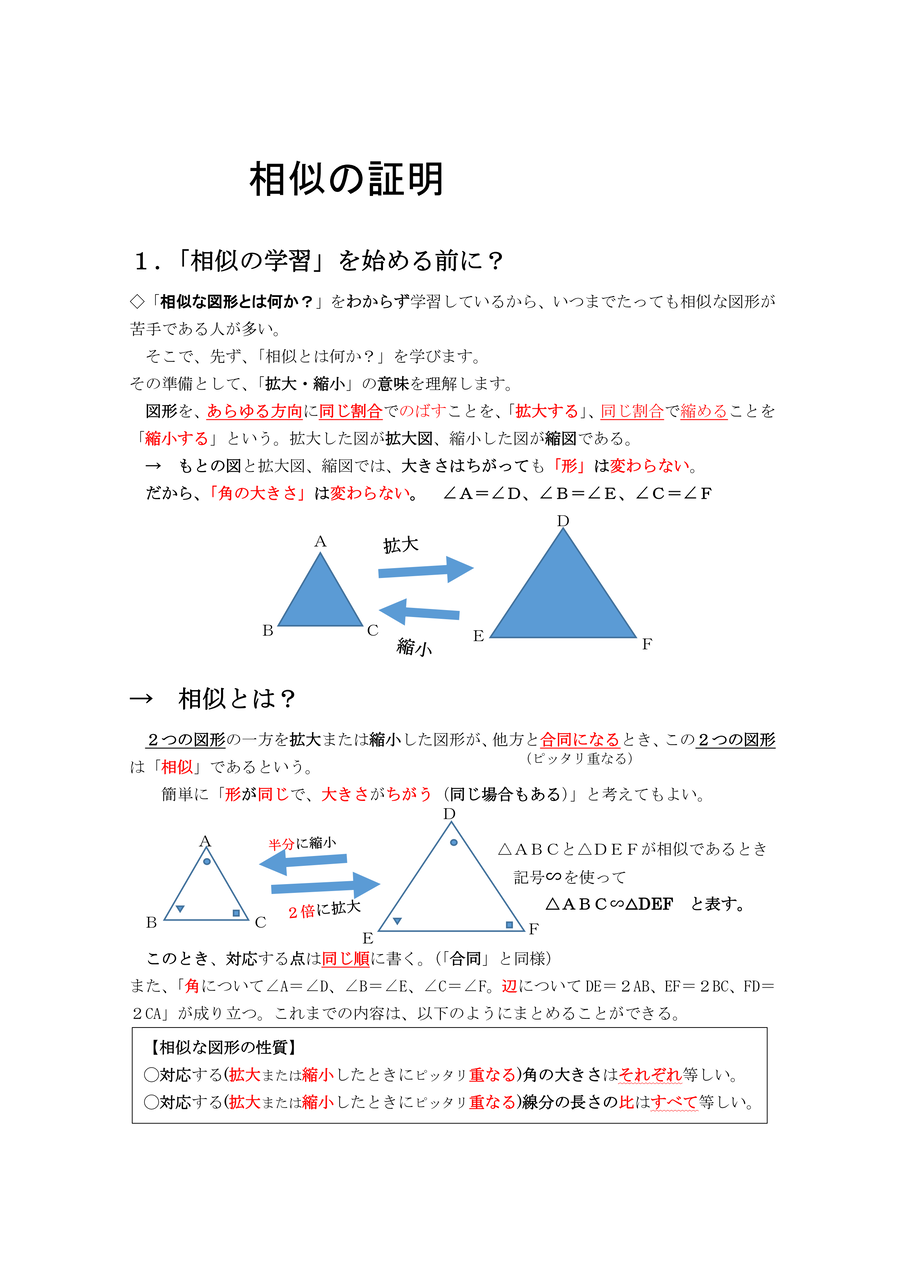世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	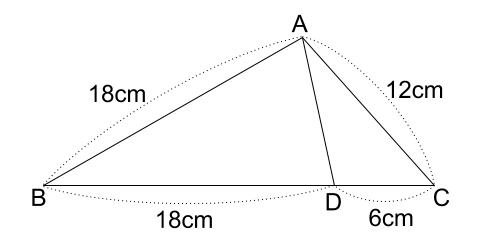世界一わかりやすい数学問題集中３ ５章 図形と相似	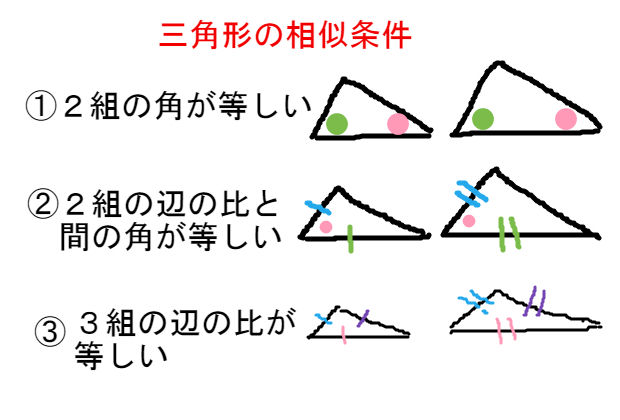世界一わかりやすい数学問題集中３ ５章 図形と相似
世界一わかりやすい数学問題集中３ ５章 図形と相似	世界一わかりやすい数学問題集中３ ５章 図形と相似

 中3数学「三角形の相似条件と証明の定期テスト過去問分析問題」 中3数学「三角形の相似条件と証明の定期テスト過去問分析問題」です。 3組の辺の比がすべて等しい。 2組の辺の比とその間の角がそれぞれ等しい。 2組の角がそれぞれ等しい。 などがあります。 しっかり、問題を文を読んで、上記の（理由）になりえないか探しましょう。 また、相似の証明では 三角形の合同条件 ①3組の辺がそれぞれ等しい ②2組の辺とその間の角がそれぞれ等しい ③1組の辺とその両端の角がそれぞれ等しい 三角形の相似条件 ①3組の辺の比がすべて等しい ②2組の辺の比が等しく、その間の角が等しい ③2組の角がそれぞれ等しい 足りないものがあったらごめん