コレクション 円 体積 公式 334352

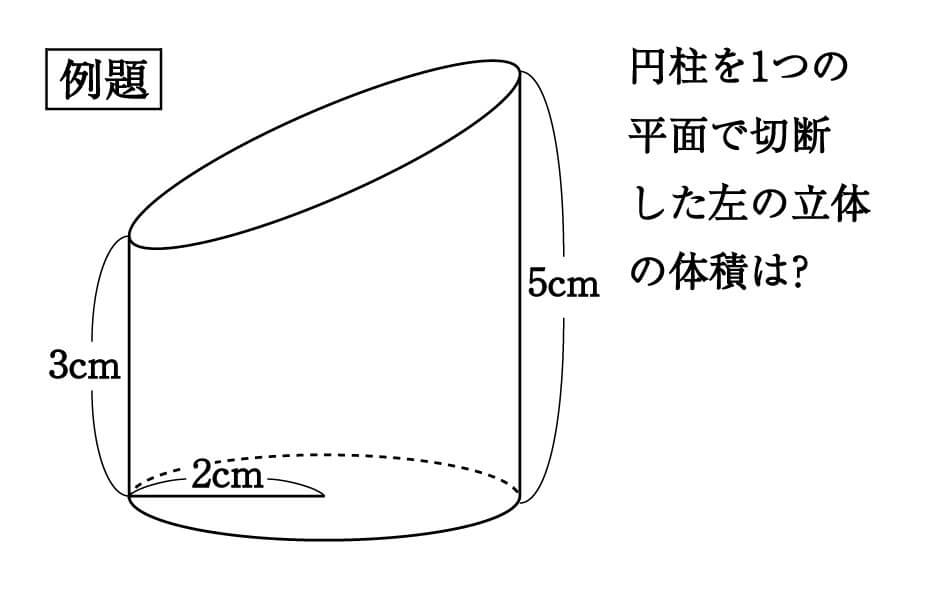
中１数学 円柱の体積 表面積はどうやって求めるの まなビタミン

 円の面積がπr^2になる納得の理由 – 図形を使った証明 18年8月29日 18年9月8日 この記事ではこんなことを紹介しています 「円の面積の公式である が、なぜそのような形で書けるか」 ここではその理由を、図形を使って視覚的に納得できる説明を紹介し 円をぐるっと 1 回転することでドーナツの形になる。 これを 円環体 と言う。 考え方としては，大きな円から小さな円の面積を引くことでドーナツの面積を求め，それを積分で積み上げることで体積を求めます。 x=t x = t として，式を変形します。 t t の

円 体積 公式

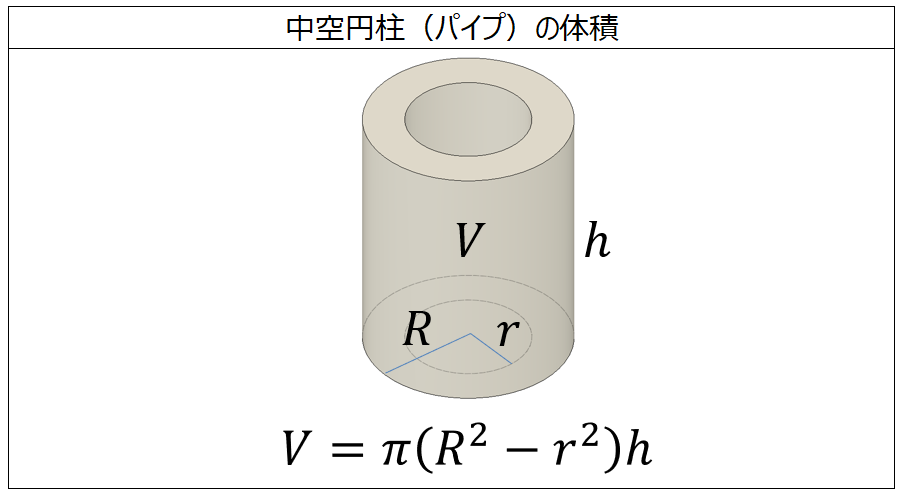
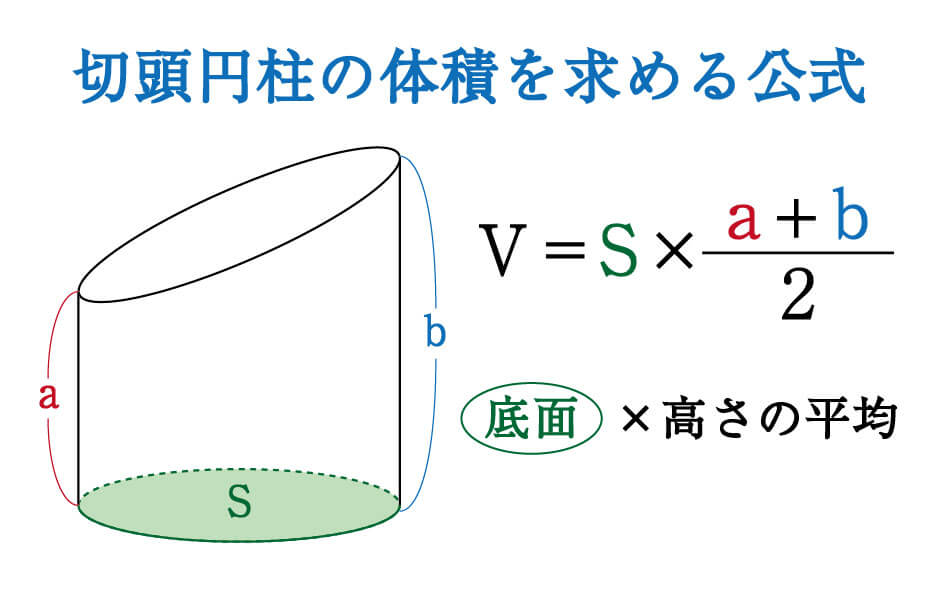
円 体積 公式-V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin 円錐の体積の求め方公式 円錐の体積は、次の公式で求められます。 円錐の体積＝底面積×高さ÷3 円錐の底面積は円の面積ですので、円の面積×高さ÷3で求めることができます。 ⇒ 円の面積の求め方 スポンサードリンク

円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ

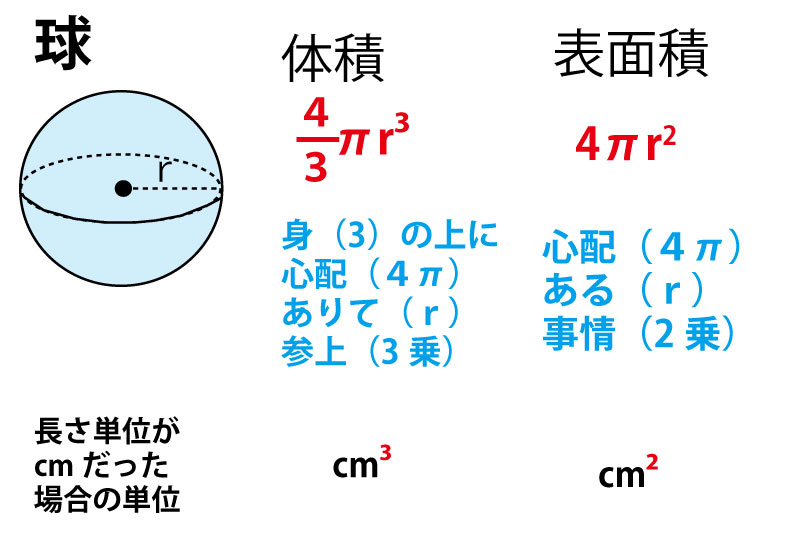
Scipursuit 体積の求め方 球 球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。 球の体積を求めるには、この公式に球の半径 r を代入すればよいだけです。 このページの続きでは 円の面積、球の体積の公式の微積による証明（導出） そもそもこれは微積を用いないと厳密には証明できない感じです。 球の体積公式まずは公式を書いておきます。半径を \(r\) として\(V=\displaystyle\frac{4}{3}\p「円」と「球」についてです。 これまでにいくつかの公式が登場してきましたね。 自信もって答えられますか？ 覚えていますか？ 円：小学校～ (円周)と(面積)の公式 球：中学校～ (表面積)と(体積)の公式

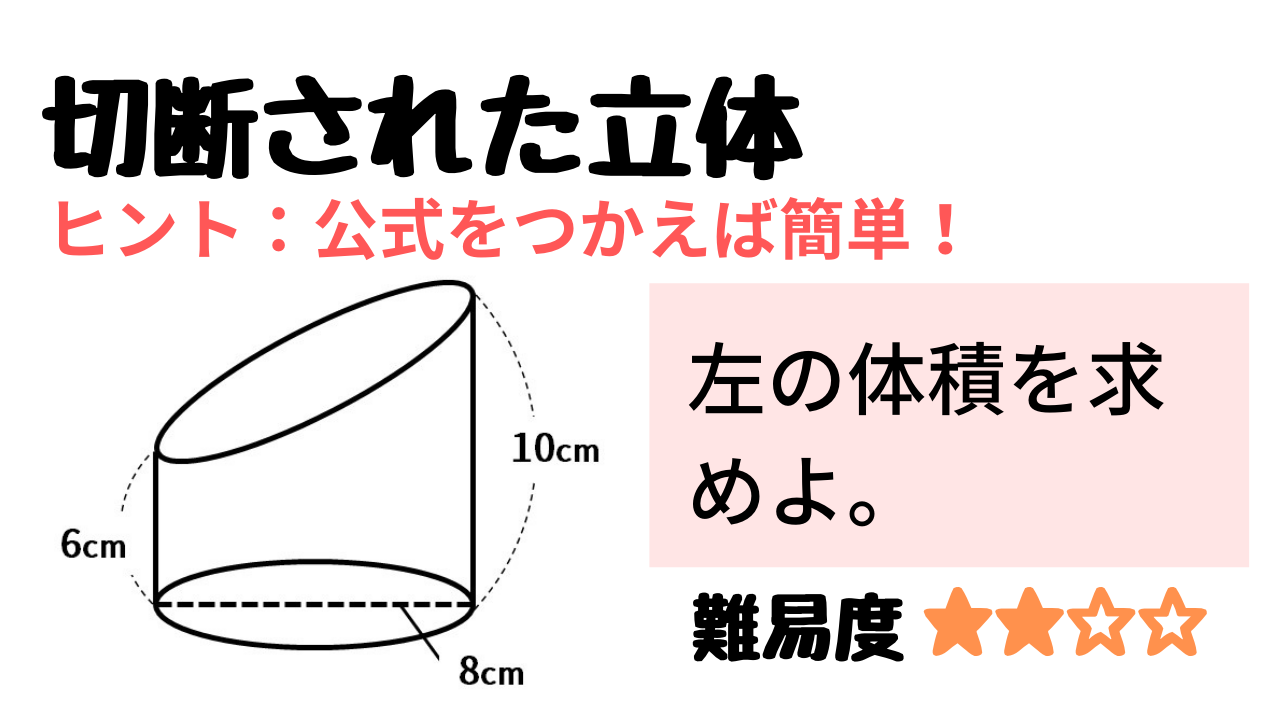
 円柱の体積＝7×7×314×12＝（cm³）となります。 答え 円柱ができる。 体積はcm³ ～立体の体積・表面積を求める公式まとめ～ 立方体・直方体の体積の求め方公式 円柱の表面積の求め方公式 三角柱の体積の求め方公式 円錐の体積円の面積の解説 円の面積は 半径×半径×円周率=面積 で求めることができます。 半径をr、円周率をπ、面積をSとすると S=πr2 となります。 円の面積を求める公式 面積=半径×半径×円周率 半径3cmの円の面積は何cm 2 ？ ※円周率を314とした場合 → 3cm×3cm×円柱の体積の解説 円柱の体積を求める公式は 半径×半径×円周率×高さ です。 円の面積が 半径×半径×円周率 なので、 円の面積×高さ とも言えます。 円柱の体積を求める公式

円 体積 公式のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	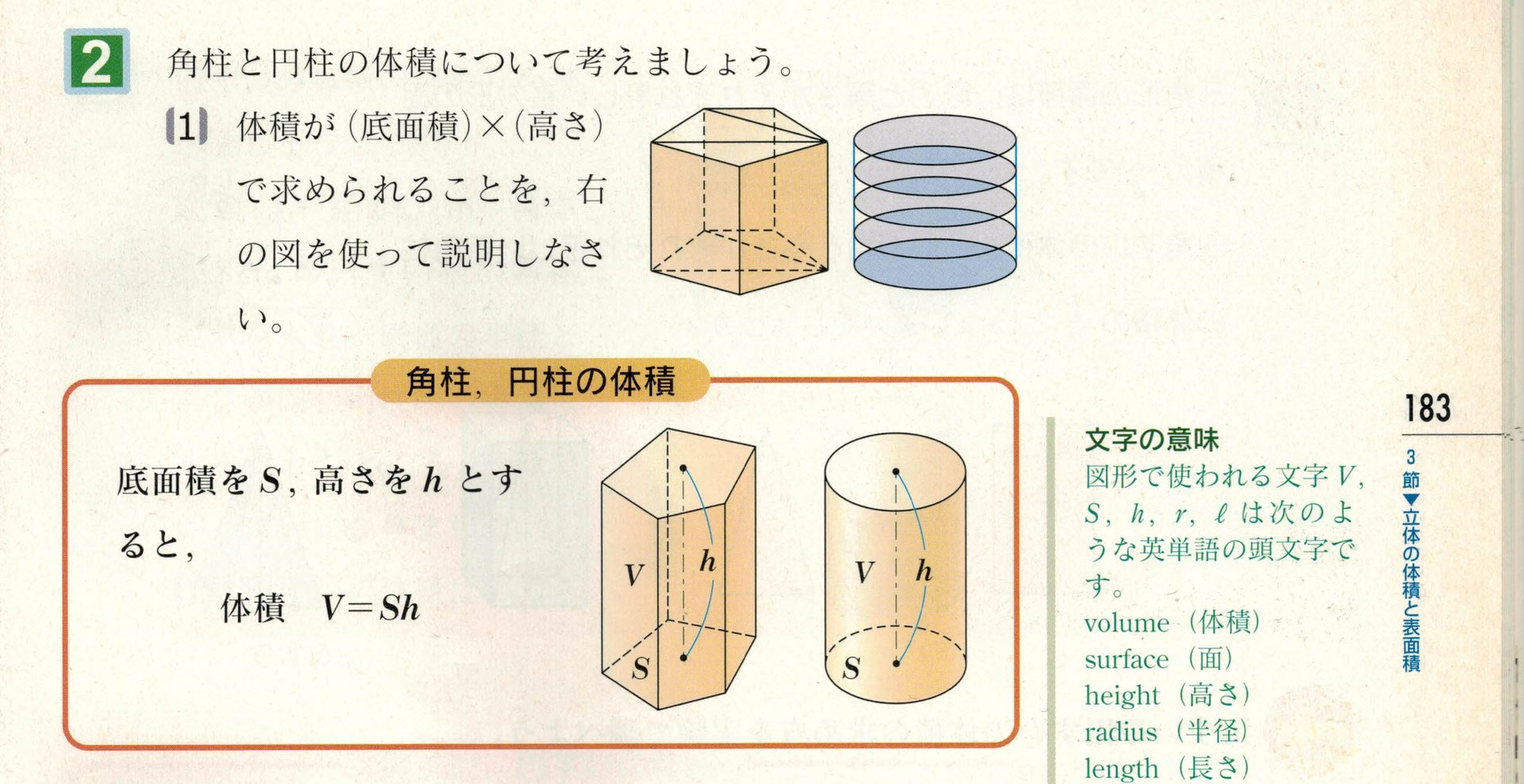半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	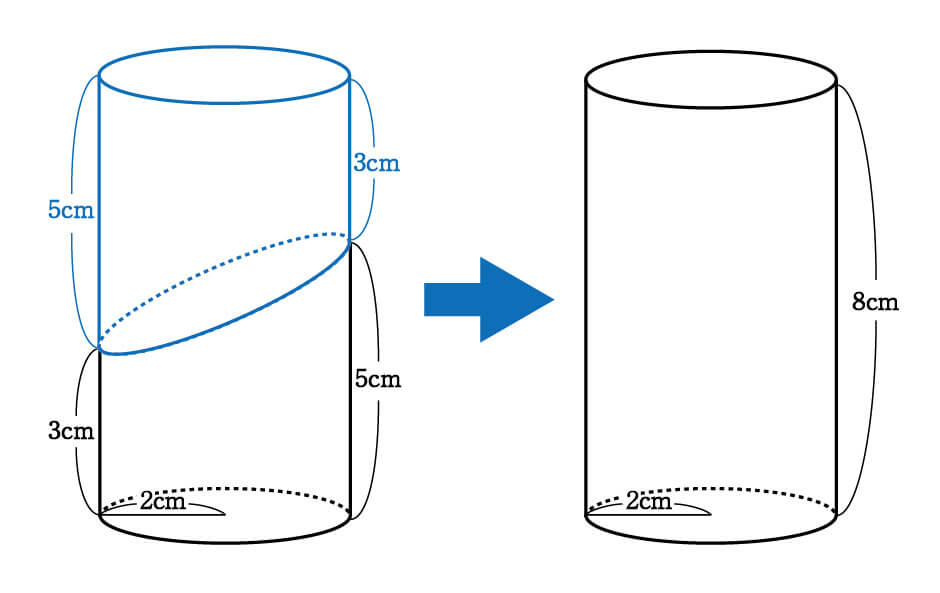半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	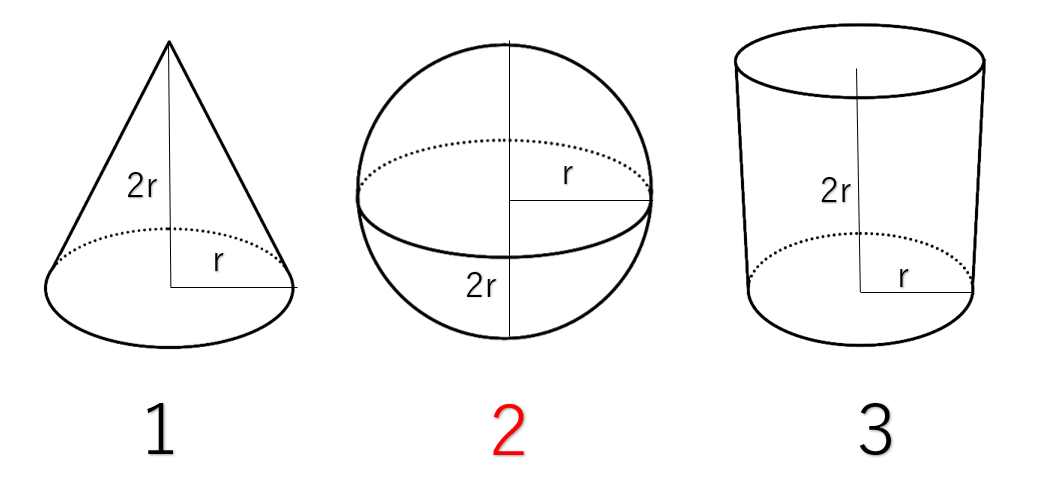半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学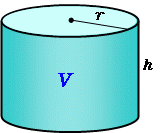
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	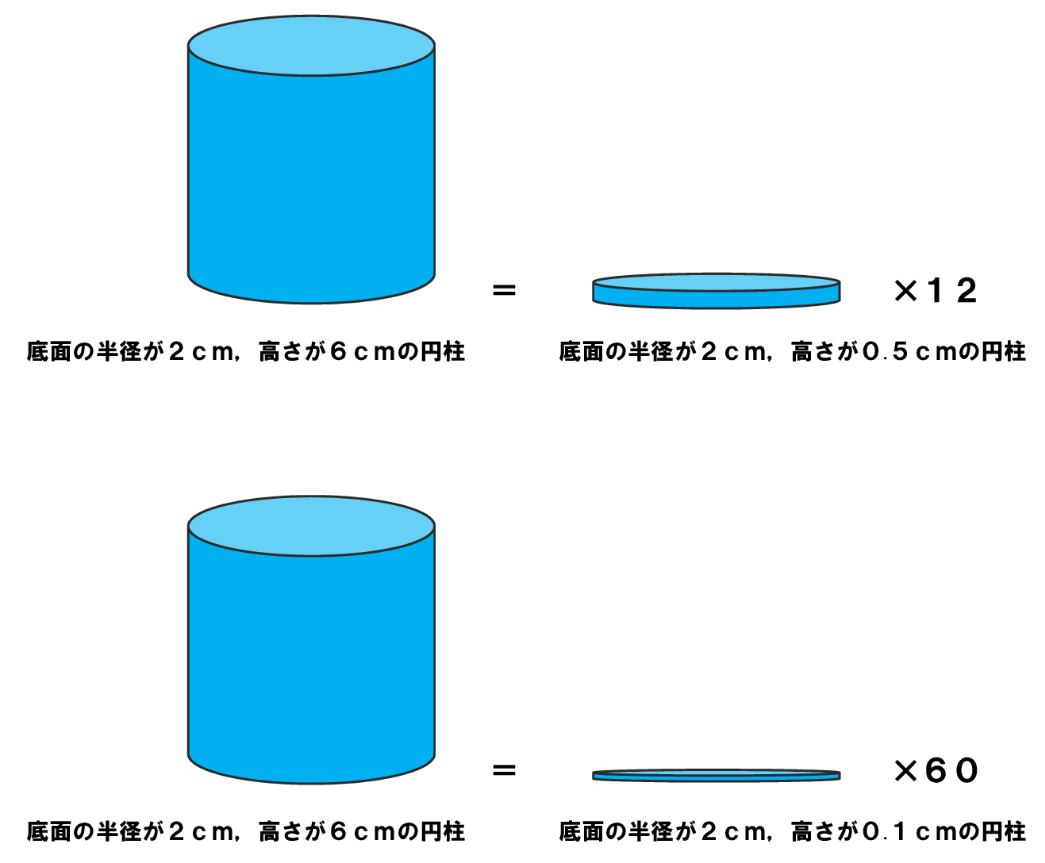半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学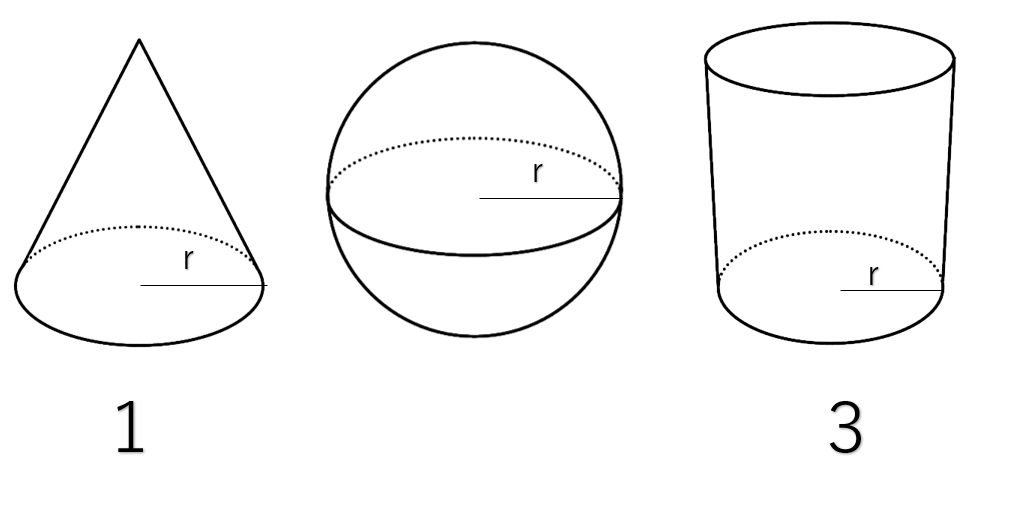
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学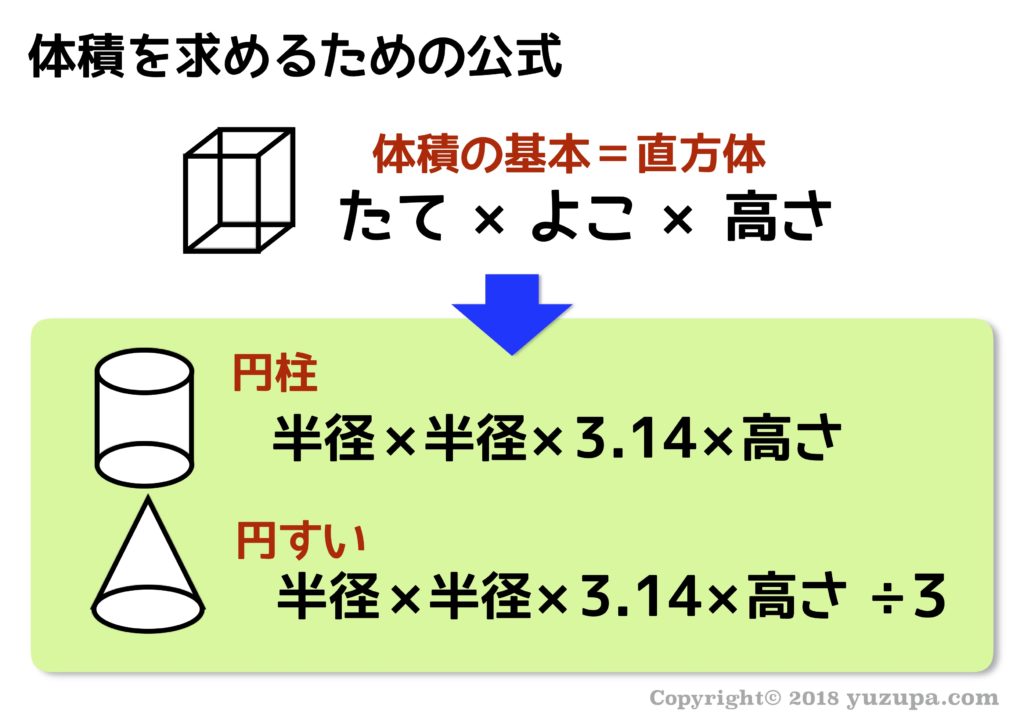
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学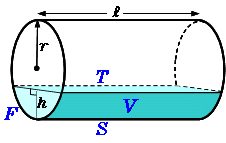
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	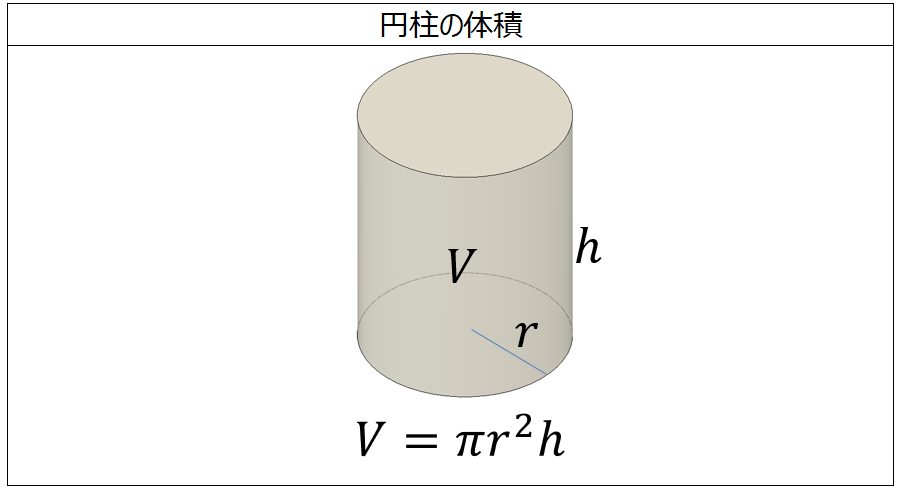半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	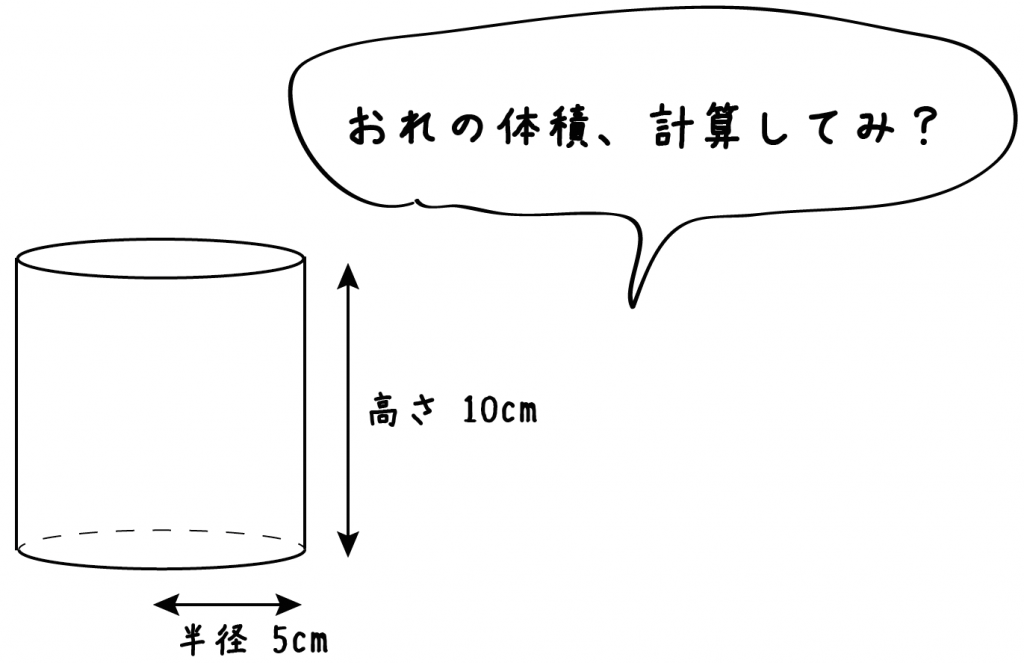半球の体積と表面積を計算する 具体例で学ぶ数学	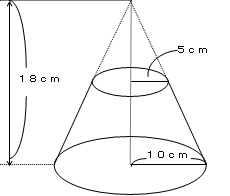半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	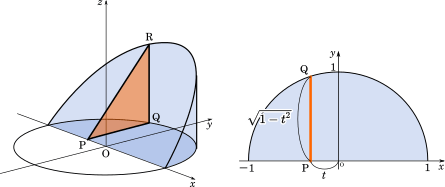半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	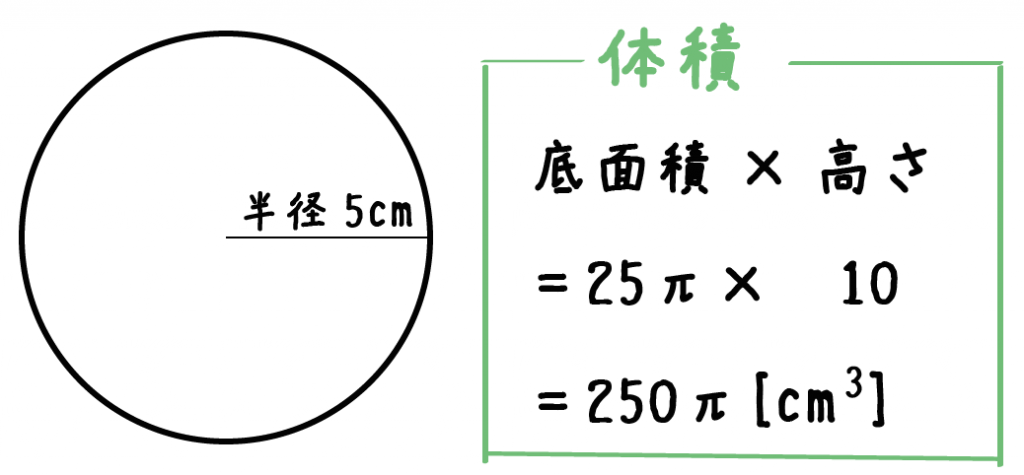半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学
半球の体積と表面積を計算する 具体例で学ぶ数学	半球の体積と表面積を計算する 具体例で学ぶ数学

直円柱の体積 そういえばこんな公式でしたね。 ケーキ型をHPに載っているものと違うものを使うにあたって、体積を知りたかった。 計算式は知っているけれどもこうやってあるととっても便利でした。 半径よりは直径のほうがいい気がしますが、普通に 円の面積の求め方と覚えるコツ。 なぜ半径×半径×314になるか 円の面積は、 「半径 × 半径 × 314」 （半径 × 半径 × 円周率 π ）という公式で求めることができます。 例題①半径 2 cmの円の面積を求めて下さい。 例題②半径 5 cmの円の面積を求めて下さい